Содержание
Вопрос перестройки логистических цепочек сегодня стал очень остро перед множеством предприятий, от малого до очень крупного бизнеса. Рассмотрим, как методы Data Science и аналитики больших данных помогают бизнесу справиться с современными вызовами на примере реализации алгоритма Дейкстры в библиотеке Graph Data Science графовой СУБД Neo4j.
Постановка задачи: поиск кратчайшего пути
Логистика и производственный менеджмент считаются наиболее популярными приложениями теории графов. Алгоритмы поиска кратчайшего пути используются при проектировании транспортных маршрутов и бизнес-операций. Представив города в виде узлов графа, их можно связать взвешенными ребрами, указав время и/или стоимость транспортировки товаров. Аналогичным образом можно представить производственные операции (поиск поставщиков, закупка, сборка, предпродажная подготовка) и/или комплектующие для итогового в виде узлов графа, также связав их между собой направленными ребрами. Таким образом, получим направленный граф свойств, который можно обработать с помощью встроенных алгоритмов графовой СУБД Neo4j. Напомним, в Neo4j граф состоит из следующих компонентов:
- Узлы (Nodes), представляющие собой объекты (сущности), которые можно промаркировать метками или ярлыками (Labels);
- отношения (Relationships)– однонаправленные специфичные связи между двумя узлами, имеющие тип и направление. Типы обеспечивают общую категорию для каждого специфичного отношения, описывающего связи узла с другими согласно контексту.
- Свойства (Properties)– конкретная информация каждого узла и отношения.
Можно определить уникальное ограничение свойства для узлов, чтобы гарантировать уникальное значение конкретной метки для каждого города. Также в Neo4j это автоматически добавляет индекс по этому полю для более быстрого импорта и запросов. Обычно таким уникальным свойством является идентификатор (id).
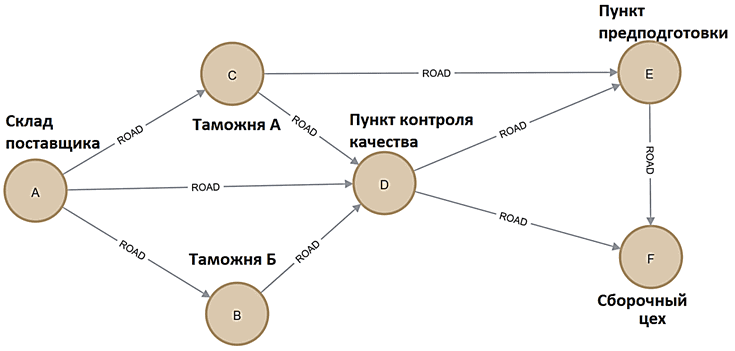
Рассмотрим логистическую задачу на поиск оптимального с точки зрения стоимости транспортного маршрута перемещения компонентов от склада поставщика до сборочного цеха через разные варианты таможни, пункты контроля качества и предварительной подготовки.
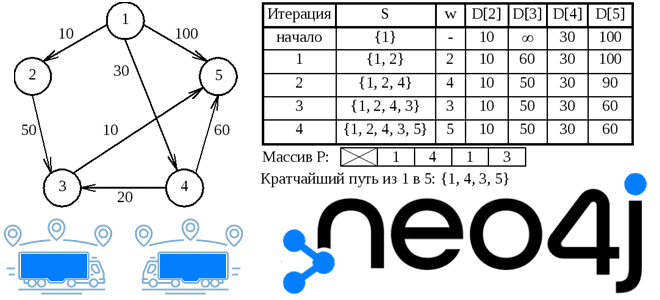
Такую типовую задачу поиска кратчайшего пути решает алгоритм Дейкстры, предложенный нидерландским учёным Эдсгером Дейкстрой в 1959 году. Алгоритм вычисляет кратчайшие пути от одной из вершин графа до всех остальных и работает только для графов, ребра которых имеют положительный вес. Этот алгоритм уже реализован в Neo4j, в библиотеке Graph Data Science, которая работает с проекциями графа в памяти — материализованным представлением сохраненного графа с ограниченной нужной информацией о свойствах. Проекции графов полностью хранятся в памяти с использованием сжатых структур данных, оптимизированных для топологии и поиска свойств. Как это работает, рассмотрим далее. А как обойтись без этой библиотеки, используя только Cypher API, читайте в нашей новой статье.
Пример реализации алгоритма Дейкстры в Neo4j-библиотеке Graph Data Science
Библиотека Graph Data Science включает 2 реализации классического алгоритма Дейкстры:
- Dijkstra Source-Target, которая вычисляет кратчайший путь между источником и целевым узлом;
- Dijkstra Single-Source для вычисления путей от исходного узла ко всем достижимым узлам.
Обе этих реализации используют двоичную кучу в качестве приоритетной очереди с использованием одного потока независимо от изменения конфигурации параллелизма. Возможно выполнение алгоритма на анонимном графе, который проецируется вместе с выполнением алгоритма.
Для работы с данными в Neo4j применяется Cypher – язык запросов, оптимизированный для графов, который определяет и исследует отношения между узлами во всех направлениях. Команды Cypher в целом похожи на SQL, но иногда отличаются. Следующий код на Cypher создает граф для рассматриваемой транспортной задачи:
CREATE (a:Location {name: 'A'}),
(b:Location {name: 'B'}),
(c:Location {name: 'C'}),
(d:Location {name: 'D'}),
(e:Location {name: 'E'}),
(f:Location {name: 'F'}),
(a)-[:ROAD {cost: 50}]->(b),
(a)-[:ROAD {cost: 50}]->(c),
(a)-[:ROAD {cost: 100}]->(d),
(b)-[:ROAD {cost: 40}]->(d),
(c)-[:ROAD {cost: 40}]->(d),
(c)-[:ROAD {cost: 80}]->(e),
(d)-[:ROAD {cost: 30}]->(e),
(d)-[:ROAD {cost: 80}]->(f),
(e)-[:ROAD {cost: 40}]->(f);
Этот граф показывает транспортную сеть с дорогами между локациями, для простоты промаркированными именем в виде латинских букв (name). Стоимость транспортировки компонентов между по разным дорогам представлена свойством отношения (cost).
Чтобы применить к этому графу Neo4j алгоритм Дейкстры из библиотеки Graph Data Science, создадим проекцию и сохраним ее в каталоге графов под именем «myGraph» с помощью следующего кода Cypher:
CALL gds.graph.create(
'myGraph',
'Location',
'ROAD',
{
relationshipProperties: 'cost'
}
)
Прежде чем начать вычисления, оценим стоимость запуска алгоритма, чтобы понять достаточно ли памяти для его выполнения на рассматриваемом графе. Если оценка покажет высокую вероятность превышения допустимых лимитов памяти, выполнение алгоритма запрещается.
MATCH (source:Location {name: 'A'}), (target:Location {name: 'F'})
CALL gds.shortestPath.dijkstra.write.estimate('myGraph', {
sourceNode: source,
targetNode: target,
relationshipWeightProperty: 'cost',
writeRelationshipType: 'PATH'
})
YIELD nodeCount, relationshipCount, bytesMin, bytesMax, requiredMemory
RETURN nodeCount, relationshipCount, bytesMin, bytesMax, requiredMemory
Результаты оценки графа из 6 узлов и 9 отношений показали необходимость 696 байт памяти, что вполне приемлемо даже для простых офисных компьютеров.
В режиме потокового выполнения алгоритм возвращает кратчайший путь для каждой пары источник-цель, позволяя проверять результаты напрямую или обрабатывать их в Cypher без каких-либо побочных эффектов. Следующий Cypher-код запустит алгоритм в потоковом режиме:
MATCH (source:Location {name: 'A'}), (target:Location {name: 'F'})
CALL gds.shortestPath.dijkstra.stream('myGraph', {
sourceNode: source,
targetNode: target,
relationshipWeightProperty: 'cost'
})
YIELD index, sourceNode, targetNode, totalCost, nodeIds, costs, path
RETURN
index,
gds.util.asNode(sourceNode).name AS sourceNodeName,
gds.util.asNode(targetNode).name AS targetNodeName,
totalCost,
[nodeId IN nodeIds | gds.util.asNode(nodeId).name] AS nodeNames,
costs,
nodes(path) as path
ORDER BY index
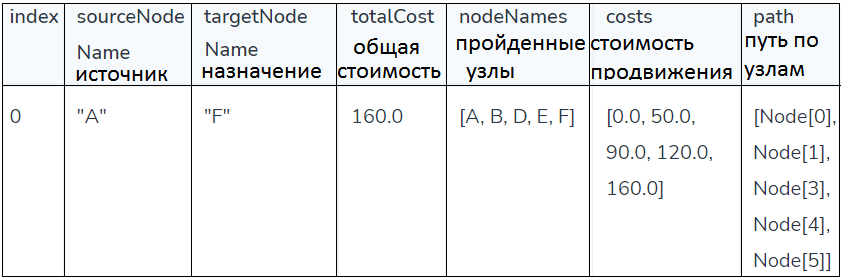
Результат выполнения покажет общую стоимость кратчайшего пути между узлом A и узлом F, включая упорядоченный список идентификаторов узлов, которые были пройдены для поиска кратчайшего пути и их совокупную стоимость.
Аналогичным образом можно построить более сложную и длинную логистическую цепочку, чтобы сравнить разные варианты транспортировки товаров по и/или времени стоимости перевозки, добавив в граф различные метки для узлов и отношений. Например, для анализа альтернатив по времени ожидания на таможне, загруженности трассы и прочих нюансов. Также можно применить этот алгоритм для анализа газотранспортной системы, о чем мы рассказываем здесь. Читайте в нашей новой статье, как повысить эффективность разработки приложений, взаимодействующих с графовой СУБД Neo4j, используя лучшие практики работы с драйверами. А в этом материале мы рассматриваем, как использовать алгоритм Дейкстры в Networkx на Google Colab.
В заключение отметим, что алгоритма Дейкстры в Neo4j работает только для графов с неотрицательными весами отношений, в отличие от алгоритма Беллмана-Форда, который мы разбираем здесь.
Больше реальных примеров применения Neo4j и других инструментов графовой аналитики больших данных для практических бизнес-задач вы узнаете на специализированных курсах в нашем лицензированном учебном центре обучения и повышения квалификации для разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков больших данных в Москве:

 384
384