Сегодня в рамках продвижения нашего нового курса по графовым алгоритмам в бизнес-приложениях, решим классическую задачу логистики в графовой базе данных Neo4j без использования методов ее специальной библиотеки Graph Data Science, а средствами Cypher-запросов.
Постановка задачи: критерии оценки для поиска кратчайшего пути
Поиск кратчайшего пути – это классическая задача на графах, которая успешно решается людьми уже несколько столетий. В настоящее время с ней успешно справляются алгоритмы, поддерживаемые в графовых базых данных. Например, в популярной NoSQL-СУБД Neo4j есть целая библиотека Graph Data Science, которая содержит множество графовых алгоритмов, включая алгоритм Дейкстры, предложенный еще в 1959 году и до сих пор активно применяемый для поиска кратчайшего пути между вершинами графа. Как использовать встроенные функции этой библиотеки, чтобы вычислить самое короткое расстояние между двумя точками, мы подробно рассказывали здесь.
Однако, сегодня попробуем решить задачу поиска наиболее выгодного пути, используя только средства встроенного языка запросов Neo4j – SQL-подобного Cypher. В качестве рабочей среды возьмем открытую GUI-консоль Neo4j, а бизнес-постановку задачу сформулируем на примере, понятном каждому жителю мегаполиса. При планировании маршрутов передвижения в городе часто возникает такая ситуация, что в какую-то точку можно добраться только пешком из-за загруженности дорог или вовсе их отсутствия. Также нередки случаи, когда при меньшей протяженности пути в километрах по времени прохождения он становится более длительным из-за автомобильных пробок, аварий или дорожных работ. Таким образом, для оценки пути с точки зрения бизнеса, например, в службе доставке или логистической компании, важно учитывать несколько критериев:
- допустимый способ перемещения (пешком или на автомобиле);
- расстояние в километрах;
- длительность прохождения этого расстояния в зависимости от способа перемещения.
Чтобы решить эту задачу, сперва создадим направленный взвешенный граф, обозначив вершины буквами, а соединяющие их ребра промаркируем несколькими отношениями, задав расстояние в километрах (distance) и время прохождения этого расстояния пешком (On_Foot) или на автомобиле (By_Car). Причем не все отношения, заданных в километрах, могут быть пройдены обоими способами передвижения. Как решить эту задачу, рассмотрим далее.
Реализация в Neo4j и Cypher
Сперва создадим в Neo4j нужный нам граф. Cypher-скрипт для создания такого графа выглядит следующим образом:
CREATE (A:Location { name: "A" })
CREATE (B:Location { name: "B" })
CREATE (C:Location { name: "C" })
CREATE (D:Location { name: "D" })
CREATE (E:Location { name: "E" })
CREATE (F:Location { name: "F" })
CREATE (G:Location { name: "G" })
CREATE (H:Location { name: "H" })
CREATE (I:Location { name: "I" })
CREATE
(A)-[:distance { km: 5 }]->(B),
(B)-[:distance { km: 10 }]->(C),
(C)-[:distance { km: 12 }]->(I),
(A)-[:distance { km: 35 }]->(D),
(D)-[:distance { km: 18 }]->(E),
(D)-[:distance { km: 7 }]->(B),
(E)-[:distance { km: 10 }]->(I),
(A)-[:distance { km: 5 }]->(F),
(F)-[:distance { km: 3 }]->(G),
(F)-[:distance { km: 6 }]->(E),
(G)-[:distance { km: 20 }]->(H),
(H)-[:distance { km: 30 }]->(I),
(A)-[:On_Foot { time: 60 }]->(B),
(B)-[:On_Foot { time: 120 }]->(C),
(C)-[:On_Foot { time: 170 }]->(I),
(C)-[:By_Car { time: 70 }]->(I),
(A)-[:By_Car { time: 35 }]->(D),
(D)-[:On_Foot { time: 120 }]->(E),
(D)-[:On_Foot { time: 90 }]->(B),
(D)-[:By_Car { time: 25 }]->(B),
(D)-[:By_Car { time: 35 }]->(E),
(E)-[:By_Car { time: 15 }]->(I),
(A)-[:By_Car { time: 2 }]->(F),
(F)-[:On_Foot { time: 60 }]->(G),
(F)-[:On_Foot { time: 70 }]->(E),
(F)-[:By_Car { time: 10 }]->(E),
(G)-[:By_Car { time: 30 }]->(H),
(G)-[:On_Foot { time: 240 }]->(H),
(H)-[:By_Car { time: 40 }]->(I)
Визуализируем этот граф в табличном виде:
match (n)-[r]-(m) return n.name, m.name, type(r), r.km, r.time ORDER BY n,m,r
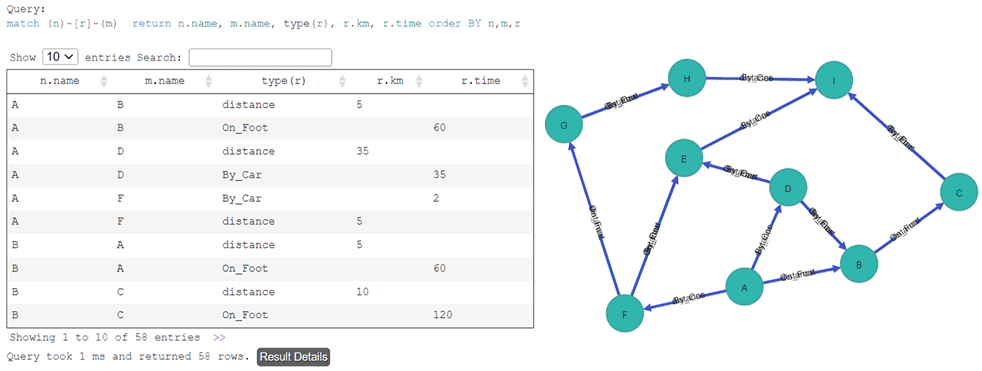
Далее составим Cypher-запрос для вычисления путей между точками А и I с указанием расстояния и длины пути, т.е. количества вершин, которые нужно обойти – за это отвечает функция length():
MATCH (from:Location { name:"A" }), (to:Location { name: "I"}) , path = (from)-[:distance*]->(to)
RETURN path AS shortestPath,
length(path),
reduce(km = 0, r in relationships(path) | km+r.km) AS totalDistance
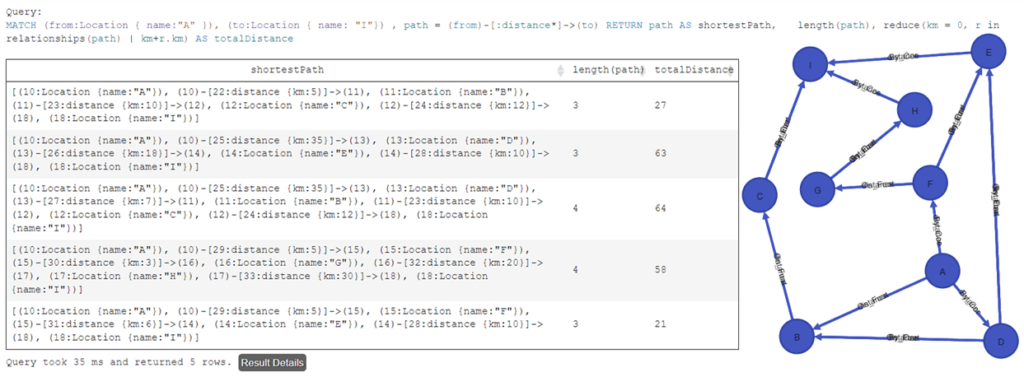
Добавим к этому запросу вычисление времени прохождении путей и сортировку по полям. А поскольку нас интересует кратчайший путь, добавим агрегатную функцию вычисления минимума от времени и расстояния. А чтобы исключить дублирование путей из-за разных отношений между некоторыми вершинами графа, добавим функцию дедубликации узлов пути distinct nodes(path).
Итоговый Cypher-запрос будет выглядеть так:
MATCH (from:Location { name:"A" }), (to:Location { name: "I"}) , path = (from)-[*]->(to)
RETURN distinct nodes(path) AS shortestPath,
length(path),
min(reduce(km = 0, r in relationships(path) | km+r.km)) AS totalDistance,
min(reduce(time = 0, r in relationships(path) | time+r.time)) AS totalTime
ORDER BY length(path), totalTime, totalDistance
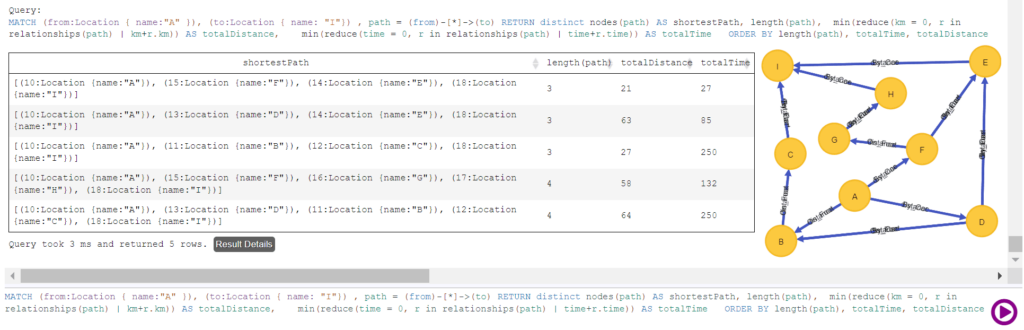
Таким образом, мы вычислили время и длительность пути между интересующими нас точками на направленном графе. Аналогичным образом можно добавить в отношение измерение стоимости прохождения пути, но тогда Cypher-запросы будут еще сложнее. Где можно еще попробовать поработать с Neo4jб читайте в нашей новой статье.
Освоить возможности практического применения графовых алгоритмов и инструментальные средства их использования в реальных проектах аналитики больших данных вам помогут специализированные курсы нашего лицензированного учебного центра обучения и повышения квалификации для разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве:
[elementor-template id=»13619″]
Источники

 671
671 

