В прошлый раз мы говорили о решении задачи классификации в рамках Machine Learning с помощью PySpark MLlib. Сегодня рассмотрим задачу регрессии. Читайте далее: что такое линейная регрессия, L1 и L2 регуляризация, алгоритм подбора значений гиперпараметров Grid Search, а также применение кросс-валидации в PySpark.
Датасет с домами на продажу
Обучать модель машинного обучения (Machine Learning) будем на датасете с домами на продажу в округе Кинг (Вашингтон, США). Его можно скачать напрямую с Kaggle или воспользоваться Kaggle API, как мы описывали здесь. Датасет содержит такие атрибуты, как цена, количество комнат, количество ванных комнат, дату постройки, площадь на квадратный фут (1 фут = 0.3 метра) и другие. Код на Python для инициализации Spark-приложения и создания DataFrame выглядит следующим образом:
from pyspark.sql import SparkSession
spark = SparkSession.builder.master("local[*]").getOrCreate()
data = spark.read.csv(
'kc_house_data.csv',
inferSchema=True, header=True)
Векторизация и разделение выборки на обучающую и тестовую
Как мы уже говорили в предыдущей статье, алгоритмы Machine Learning в PySpark принимают на вход только вектора, поэтому нам необходимо предварительно векторизовать данные.
Мы будем обучать модель на 5 признаках: площадь на квадратный фут, количество комнат, количество ванных комнат и дата постройки. Отберем их с помощью метода select:
features = ['sqft_living', 'bedrooms',
'bathrooms', 'yr_built']
target = 'price'
attributes = features + [target]
sample = data.select(attributes)
А чтобы векторизовать выбранные признаки, воспользуемся классом VectorAssembler. Он принимает в качестве аргументов список признаков, которые необходимо преобразовать в вектор, и название преобразованного вектора. Вот так это выглядит в Python:
from pyspark.ml.feature import VectorAssembler
assembler = VectorAssembler(inputCols=features,
outputCol='features')
output = assembler.transform(sample)
Теперь разобьём выборку на обучающую и тестовую. На обучающей создадим модель Machine Learning, а на тестовой проверим эффективность этой модели. Причём, разделим данные в пропорции 9:1. Python-код:
train, test = output.randomSplit([0.9, 0.1])
Grid Search: оптимизация гиперпараметров
Одна из задач машинного обучения является подбор гиперпараметров, которые задает Data Scientist перед обучением. У каждого алгоритма Machine Learning они свои. Однако подбирать их вручную утомительно и затратно, поэтому существуют специальные алгоритмы подбора. В PySpark встроен один из таких алгоритмов — Grid Search.
Grid search есть не что иное, как комбинация из всех значений заданных гиперпараметров. Например, пусть имеется два гиперпараметра: первый может принимать 2 значения, а второй — 3. Тогда возможно всего 6 комбинаций:
a = [1, 2]
b = [3, 4, 5]
grid_search = [(1,3), (1,4), (1,5),
(2,3), (2,4), (2,5)]
Гиперпараметры линейной регрессии в PySpark
В модуле MLlib имеется класс LinearRegression, который отвечает за линейную регрессию. У него есть два основных гиперпараметра:
-
regParam;
-
elasticNetParam.
Эти параметры задают вид регуляризации: L1 или L2. Единственное, что делает регуляризация — это добавляет ещё один параметр к целевой функции, а обучение остаётся тем же самым. Как известно, цель машинного обучения минимизировать целевую функцию. В линейной регрессии целевая функция — это сумма квадратов остатков [1]. Она определяется как:
RSS = sum((y_real - y_predicted)**2)
В L1-регуляризации к целевой функции добавляется сумма весов, и такая регуляризация называется Lasso. Выражается она так:
RSS = sum((y_real – y_predicted)**2) lasso = RSS + theta * sum(W)
В L2-регуляризации к целевой функции добавляется сумма квадратов весов, и такая регуляризация называется Ridge. Выражается она так:
RSS = sum((y_real – y_predicted)**2) ridge = RSS + lambda * sum(W*W)
Кроме того, эти два вида регуляризации можно соединить вместе, и такая регуляризация называется Elastic Net.
В линейной регрессии без регуляризации предполагается, что коэффициенты регрессии (веса) могут равновероятно принимать любые значения. В L1 регуляризации предполагается, что эти коэффициенты распределены по закону Лапласа, в L2 — по закону Гаусса. И та, и другая регуляризация не даёт весам быть слишком большими, и, возможно, повысится обобщающая способность модели.
Обобщенная формула для регуляризации в PySpark
В Python-библиотеке Scikit-learn все виды регуляризации линейной регрессии разделены по соответствующим классам Lasso, Ridge и ElasticNet. Но в PySpark это реализовано в общем виде и зависит от гиперпарметров regParam и elasticNetParam. Выражается это так:
L1 = W L2 = W*W reg = regParam * (elasticNetParam * L1 + (1 - elasticNetParam) * L2)
Таким образом, задавая определённые значения regParam и elasticNetParam, можно получить следующие результаты:
-
regParam = 0 — это линейная регрессия без регуляризации;
-
regParam > 0, elasticNetParam = 0 ведет к L2-регуляризация (Ridge);
-
regParam > 0, elasticNetParam = 1 ведет к L1-регуляризация (Lasso);
-
regParam > 0, 0 < elasticNetParam < 1 ведет к L1 + L2 (Elastic Net).
Создаем модель и задаем гиперпараметры с помощью Grid Search
Прежде всего создадим модель линейной регрессии из модуля Spark MLlib. Нужно указать название векторизованного атрибута и целевой атрибут, значения которого нужно предсказать. В нашем случае мы пытаемся предсказать цену на дом. Python-код:
from pyspark.ml.regression import LinearRegression
lin_reg = LinearRegression(
featuresCol='features',
labelCol='price')
Для инициализации Grid Search в PySpark используется класс ParamGridBuilder. В метод addGrid добавляются гиперпарметр и значения, которые он может принимать. Выберем 3 значения для regParam и два значения для elasticNetParam. Так это выглядит в Python:
grid_search = ParamGridBuilder() \
.addGrid(lin_reg.regParam, [0.0, 0.01, 0.1]) \
.addGrid(lin_reg.elasticNetParam, [0.5, 1.0]) \
.build()
Метрика качества
Нам также нужно указать метрику качества для оценки модели. Для задачи регрессии используется RegressionEvaluator, который по умолчанию в качестве метрики использует среднюю квадратическую ошибку (MSE). MSE можно поменять на среднюю абсолютную ошибку (MAE). Кроме того, мы должны указать названия целевого и предсказанного атрибутов. Линейная регрессия в PySpark после обучения создает предсказанный атрибут под название prediction, а целевая так и остаётся price. Python-код выглядит так:
evaluator = RegressionEvaluator(predictionCol='prediction',
labelCol='price')
Кросс-валидация
В предыдущей статье у нас был большой датасет, поэтому мы разбили его только на обучающую и тестовую выборки. Сегодняшний датасет небольшой, поэтому воспользуемся кросс-валидацией. С помощью кросс-валидации данные разделяются на N блоков, обучение происходит по N-1 блокам, а оставшийся блок уходит на валидационную выборку. После каждой итерации изменятся блок валидации. Рисунок ниже показывает такую процедуру для N=3.
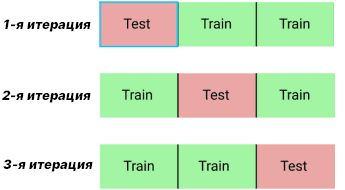
В PySpark кросс-валидация реализуется через CrossValidator. В нем нам нужно указать три аргумента:
-
estimator— модель Machine Learning, в нашем случае линейная регрессия; -
estimatorParamMaps— алгоритм оптимизации гиперпараметров, в нашем случае Grid Search; -
evaluator— метрика качества, в нашем случае RegressionEvaluator.
Также можно указать в аргументах numFolds — количество блоков N (по умолчанию их 3). После указания значений этих аргументов вызывается метод fit для выполнения кросс-валидации. В Python это выглядит следующим образом:
cv = CrossValidator(estimator=lin_reg,
estimatorParamMaps=grid_search,
evaluator=evaluator)
cv_model = cv.fit(train)
Результаты кросс-валидации
Мы можем посмотреть модель с теми гиперпараметрами, которые показали наибольшую эффективность или, если быть точнее, наименьшее значение функции потерь. Для этого есть атрибут bestModel, который хранит информацию о лучшей модели.
Мы можем посмотреть, например, на среднюю абсолютную ошибку:
cv_model.bestModel.summary.meanAbsoluteError # 145260.09296909513
А также извлечь параметры этой модели. Нас больше интересует параметры регуляризации:
cv_model.bestModel.extractParamMap()
#
{
Param(parent='LinearRegression_b64ded0857c9', name='elasticNetParam', doc='the ElasticNet mixing parameter, in range [0, 1]. For alpha = 0, the penalty is an L2 penalty. For alpha = 1, it is an L1 penalty'): 1.0,
Param(parent='LinearRegression_b64ded0857c9', name='regParam', doc='regularization parameter (>= 0)'): 0.1,
}
Как видим, лучшая модель имеет гиперпараметр elasticNetParam равный 1, а regParam — 0.1. Значения этих параметров показывают, что лучшая модель использует L1-регуляризацию (regParam > 0, elasticNetParam=1).
Больше подробностей о линейной регрессии, L1 и L2 регуляризации, алгоритмах подбора гиперпараметрах, а также о кросс-валидации в PySpark на примерах задач Data Science и Big Data вы узнаете на наших практических курсах по Apache Spark и Machine Learning в лицензированном учебном центре обучения и повышения квалификации разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве:
- Анализ данных с Apache Spark
- Введение в машинное обучение на Python
- Введение в нейронные сети на Python
Источники