Содержание
Продвигая наш новый курс по графовым алгоритмам в бизнес-приложениях, сегодня рассмотрим применение теории графов к задаче анализа социальных связей на практическом примере возможностей библиотеки Graph Data Science СУБД Neo4j и ее языка запросов Cypher. А также разберем сопутствующую теорию: что такое центральность графа, почему эта мера не подходит для сетей со сложной топологией и какие показатели использовать вместо нее.
Ключевые понятия теории графов для анализа социальных связей
Анализ социальных связей – одно из самых востребованных приложений теории графов. К примеру, в пользователей социальной сети можно представить вершинами (узлами) графа, связав знакомых людей ребрами (связями). Эту идею можно применить не только для вычисления самого популярного блогера или его поста, но и для выявления неформальных лидеров в крупных организациях. Направленные графы могут показывать авторитет и уровень полномочий, а также силу влияния отдельного человека на принятие управленческих решения. Внутри организаций социальные исследователи выделяют несколько типов сетей:
- сети советов, куда входят сотрудники, от которых зависит принятие решений;
- сети доверия для обмена важной «закулисной» информацией;
- сети коммуникации, которые выявляют цепи коммуникации сотрудников по вопросам, связанным с работой.
Все эти сети существуют в неформальной организации одновременно, определяя общую динамику организационной культуры и изменения организационного знания. Содержание передаваемых данных, передаваемых по таким сетям может быть различным: объективная информация, эмоции, предположения и пр.
Обычно для анализа социальных связей исследуются несколько характеристики графа:
- степень связности — число связей, инцидентных узлу, т.е. количество его ребер. В направленном графе определяются две меры степени связности: полустепень захода (число связей, входящих в узел) и полустепень исхода (число связей, исходящих из узла). Например, если рассматривать связь как дружбу или сотрудничество, полустепень захода показывает популярность человека, а полустепень исхода – его общительность. Не стоит путать степень связности вершины с компонентами сильной или слабой связности графа, о чем мы рассказываем здесь. Центральность по Кацу – это обобщение степени связности, которая измеряет не число прямых соседей, а число всех узлов, которые могут быть связаны путями, при штрафовании дальних узлов.
- Степень родства – число связей конкретного узла с другими;
- нормализованная степень близости узла равна средней длине кратчайшего пути между узлом и всеми другими узлами в графе.
Применительно к анализу социальных связей в организации можно выделить меру эффективности, которая показывает, насколько высокой должна быть плотность сети, чтобы поддерживать связь внутри социальной группы, даже если ее участники не связаны друг с другом напрямую. Также в этой задаче важен показатель центральности или близости к центру, который определяет наиболее важные вершины графа, т.е. наиболее влиятельных лиц. Чем центральнее узел, тем ближе он ко все остальным узлам. С понятием центральности связаны следующие меры:
- степень посредничества – мера центральности вершины в графе, число раз, когда узел служит мостом в кратчайшем пути между двумя другими узлами, показывает меру количественного выражения взаимодействия человека с другими людьми в социальной сети.
- степень влиятельности — мера влияния узла в сети в зависимости от его связей с другими узлами – связи с узлами с высоким показателем влиятельности вкладывают больше в показатель рассматриваемого узла, чем такая же связь с узлом с низким показателем.
Важно, что аккуратность меры центральности зависит от топологии сети, а сложные сети имеют неоднородную топологию. Поэтому меры центральности, пригодные для выявления узлов с высокой степенью влиятельности, скорей всего, будут непригодны для остатка сети. Из-за этого для вычисления влиятельности в сетях со сложной топологией используют показатель доступность, который измеряет измеряет разброс невозвратных блужданий (последовательность смежных вершин, посещаемых однократно), начинающихся с данного узла.
Рассмотрим пример вычисления некоторых из этих мер с помощью языка запросов Cypher в графовой базе данных Neo4j.
Пример определения меры центральности в Neo4j с Cypher
Библиотеки Graph Data Science включает множество готовых алгоритмов, включая алгоритмы определения центральности. Сперва создадим в Neoj4 следующий граф социальных связей из 6 пользователей, связанных между собой отношениями подписки:
CREATE
(alice:User {name: 'Alice'}),
(bridget:User {name: 'Bridget'}),
(charles:User {name: 'Charles'}),
(doug:User {name: 'Doug'}),
(mark:User {name: 'Mark'}),
(michael:User {name: 'Michael'}),
(alice)-[:FOLLOWS {score: 1}]->(doug),
(alice)-[:FOLLOWS {score: -2}]->(bridget),
(alice)-[:FOLLOWS {score: 5}]->(charles),
(mark)-[:FOLLOWS {score: 1.5}]->(doug),
(mark)-[:FOLLOWS {score: 4.5}]->(michael),
(bridget)-[:FOLLOWS {score: 1.5}]->(doug),
(charles)-[:FOLLOWS {score: 2}]->(doug),
(michael)-[:FOLLOWS {score: 1.5}]->(doug)
Записав граф в Neo4j, его можно спроецировать в каталог графов, чтобы подготовить к выполнению алгоритма, используя собственную проекцию, нацеленную на узлы User и отношения FOLLOWS.
CALL gds.graph.create(
'myGraph',
'User',
{
FOLLOWS: {
orientation: 'NATURAL',
properties: ['score']
}
}
)
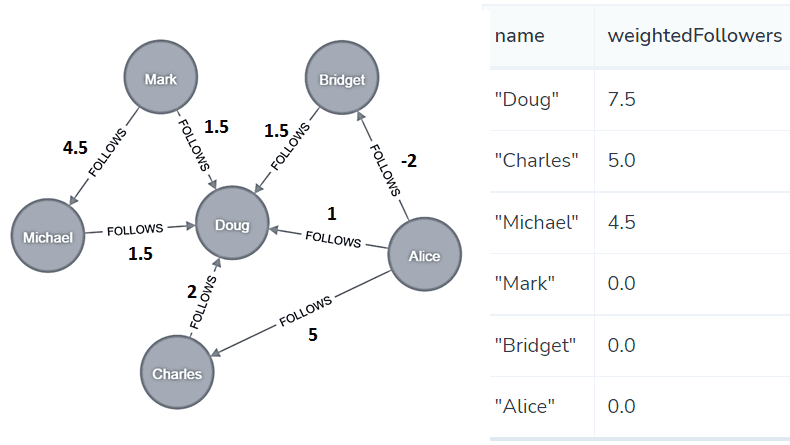
По умолчанию алгоритм определения центральности узлов в библиотеке Graph Data Science СУБД Neoj4 использует естественную ориентацию (NATURAL) для вычисления степеней. В данном примере ориентация NATURAL поможет определить самого популярного человека в этой социальной сети, т.е. блогера с максимальным числом подписчиков. В прямой ориентации пользователь Doug занимает центральное место в сети, имея максимум подписчиков: 5 из 5 возможных, кроме него самого. Это подтверждается значениями взвешенной меры центральности, которая измеряет сумму положительных весов входящих и исходящих отношений. Вычислить ее поможет следующий Cypher-запрос:
CALL gds.degree.stream(
'myGraph',
{ relationshipWeightProperty: 'score' }
)
YIELD nodeId, score
RETURN gds.util.asNode(nodeId).name AS name, score AS weightedFollowers
ORDER BY weightedFollowers DESC, name DESC
Но иногда есть смысл проанализировать другую ориентацию, например, чтобы узнать, на сколько аккаунтов подписан каждый пользователь. Изменить ориентацию можно с помощью свойства конфигурации orientation, принимающее значение по умолчанию прямой (NATURAL), обратной (REVERSE) и ненаправленной (UNDIRECTED).
Следующий код на Cypher запустит алгоритм в потоковом режиме, показывая, какие пользователи имеют наивысшую степень центральности, используя обратную ориентацию отношений:
CALL gds.degree.stream(
'myGraph',
{ orientation: 'REVERSE' }
)
YIELD nodeId, score
RETURN gds.util.asNode(nodeId).name AS name, score AS followees
ORDER BY followees DESC, name DESC
Таким образом, в обратной ориентации пользователь Alice занимает более центральное место в сети, чем Doug.

Наконец, покажем, как оценить стоимость запуска алгоритма, чтобы понять влияние алгоритма на потребление. Если оценка покажет высокую вероятность, что выполнение алгоритма превысит доступные ограничения памяти, то оно запрещается.
CALL gds.degree.write.estimate('myGraph', { writeProperty: 'degree' })
YIELD nodeCount, relationshipCount, bytesMin, bytesMax, requiredMemory
Как реализовать это самостоятельно в веб-консоли этой графовой СУБД, читайте в нашей новой статье.
Читайте в нашей следующей статье про анализ графов NFT-транзакций с Neo4j и Cypher. Пример улучшения рекомендательной системы с помощью этих инструментов мы разбираем здесь. А еще больше практических подробностей про использование Neo4j и Cypher для графовой аналитики больших данных в бизнес-приложениях вы узнаете на специализированных курсах в нашем лицензированном учебном центре обучения и повышения квалификации для разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков больших данных в Москве:
[elementor-template id=»13619″]
Источники

 634
634 

