Проблемы анализа данных временных рядов и способы их решения: какие статистические методы и алгоритмы глубокого обучения лучше подходят для прогнозирования.
Особенности прогнозирования временных рядов
Напомним, временным рядом считается набор данных, каждая точка которого привязана ко времени (час, минуты, дни, месяцы, годы и прочие периоды). Эти данные имеют динамический характер и обязательное значение атрибута DateTime, который используется для их индексации. Хотя большинство алгоритмов машинного обучения являются оценщиками максимального правдоподобия и имеют статистический характер, их принципы работы в прогнозировании временных рядов отличаются от классической статистики. При этом традиционные статистические модели, в т.ч. алгоритмы авторегрессии, могут быть определены как линейная регрессия по задержкам ряда, а линейная регрессия обычно считается ML-алгоритмом.
Однако, применение алгоритмов глубокого обучения к данным временных рядов, чтобы делать прогнозы для будущих значений DateTime, например, предсказать продажи на будущий февраль по данным за предыдущие 5 лет, отличается от использования статистических методов. При этом некоторые этапы у них похожи. В частности, удаление пропусков является ключевым этапом предварительной обработки в любом проекте Machine Learning. В статистике пропуски обычно заполняются средним значением, медианой или модой в зависимости от характера атрибута, или используются более сложные методы, такие как алгоритм ближайших соседей, о котором мы недавно писали здесь.
Однако, при прогнозировании будущих значений в анализе временных рядов вместо матожидания (среднее статическое при нормальном распределении случайной величины) используется скользящее среднее в рамках какого-то периода. Это также характерно для потоковой обработки данных «на лету» без пакетной агрегации. Скользящее среднее может заполнить пропуски в данных временного ряда. Скользящее среднее не стоит путать с интерполяцией, которая тоже часто используется для заполнения пропусков, вычисляя их значения по предыдущим и последующим точкам. Например, линейная интерполяция работает путем вычисления прямой линии между двумя точками, их усреднения и получения отсутствующих данных. Хотя современные Data Science библиотеки поддерживают различные методы интерполяции (Linear, Spline, Stineman и пр.), в прогнозировании временных рядов они применяются не очень часто, т.к. эти динамические данные имеют следующие особенности:
- тенденция изменения (рост или падение);
- сезонность – периодические закономерности, повторяющиеся с постоянной частотой;
- цикличность, характерная для трендов без заданных повторений или сезонности;
- стационарность – данные временного ряда являются стационарными, если их статистические характеристики не меняются с течением времени, т. е. постоянное среднее значение и стандартное отклонение остаются неизменными, а ковариация не зависит от времени.
Эти характеристики очень важны для анализа переменных временного ряда, чтобы понять их поведение, выявить закономерности она имеет, а также выбрать наиболее подходящую модель. Кроме того, для данных временных рядов характерна частичная автокорреляция, которая является мерой связи между текущими и прошлыми значениями рядов и указывает, какие прошлые значения рядов наиболее полезны для прогнозирования будущих значений. Эти особенности исследуемых данных обусловливают выбор подходящих методов для их анализа, что мы и рассмотрим далее.
Алгоритмы анализа данных временных рядов
Прежде всего, перечислим некоторые популярные алгоритмы для прогнозирования временных рядов:
- ARIMA — авторегрессивное интегрированное скользящее среднее;
- EWMA — экспоненциально взвешенное скользящее среднее, которое уменьшает эффект запаздывания, проявляемого скользящими средними, путем придания большего веса значениям, которые произошли совсем недавно;
- динамическая регрессия, которая учитывает другую разнообразную информацию, такую как государственные праздники, изменения в законодательстве и прочие события внешнего контекста;
- LSTM (Long Short-Term Memory) — тип рекуррентной нейросети, которая может изучать зависимость порядка между элементами в последовательности.
Это далеко не полный перечень. Сюда же относятся обобщенная авторегрессионная условная гетероскедастичность (GARCH, Generalized Autoregressive Conditional Heteroskedasticity) и байесовские структурные временные ряды, а также авторегрессионные нейросети (NNAR, Neural Networks Autoregression), которые можно применять к временным рядам, которые используют предикторы с запаздыванием и могут обрабатывать фичи.
Важно помнить, что работа с фичами отличает алгоритмы Deep Learning от классической статистики для анализа данных временных рядов. В статистике обычно используются преобразование признаков, масштабирование, сжатие, нормализация, кодирование и прочие методы подготовки данных. Однако, данные временных рядов могут иметь другие атрибуты, помимо фичей, привязанных ко времени. Если эти атрибуты также связаны со временем, результирующий временной ряд будет многомерным. В статистике результат будет одномерным со статическими фичами, не зависящими от времени.
Статистическая модель предписывает процесс генерации данных, например, авторегрессия рассматривает только взаимосвязь между лагами ряда и его будущими значениями. А модель глубокого обучения изучает эту связь, становясь более общей, например, нейросеть создает свои собственные фичи, используя нелинейные комбинации входных данных. DL-алгоритмы более требовательны к данным и вычислительным ресурсам, чем статистические методы.
Прежде чем сравнивать статистические методы машинного обучения с алгоритмами Deep Learning, следует определиться с мерам такого сравнения. Обычно в качестве таких мер используются метрики ошибки прогнозирования:
- ошибки, зависящие от масштаба — средняя абсолютная ошибка (MAE, Mean Absolute Error) и среднеквадратичная ошибка (RMSE, Root Mean Squared Error);
- ошибки в процентах — средняя абсолютная ошибка в процентах (MAPE, Mean Absolute Percentage Error) и симметричная MAPE-ошибка (SMAPE, Symmetric Mean Absolute Percentage Error);
- масштабированные ошибки — средняя абсолютная ошибка в процентах (MASE, Mean Absolute Scaled Error).
Впрочем, хотя эти метрики оценки помогают определить, насколько близки подобранные значения к фактическим, они не оценивают качество соответствия модели всему временному ряду.
Как показывают многочисленные исследования, пока алгоритмы ETS и ARIMA более точны, чем методы глубокого обучения. При этом статистические методы машинного обучения показывают лучшие результаты, чем Deep Learning на краткосрочных периодах прогнозирования. Период прогнозирования вообще очень важен для анализа временных рядов. В большинстве случаев DL-алгоритмы менее точны, чем статистические модели для коротких и средних временных горизонтов. Но эти различия снижаются по мере увеличения горизонта прогнозирования. Например, модель Theta более точна, чем модели Feed-Forward, Transformer и WaveNet для краткосрочных и среднесрочных прогнозов, а также лучше, чем модели Feed-Forward и Transformer для долгосрочных прогнозов.
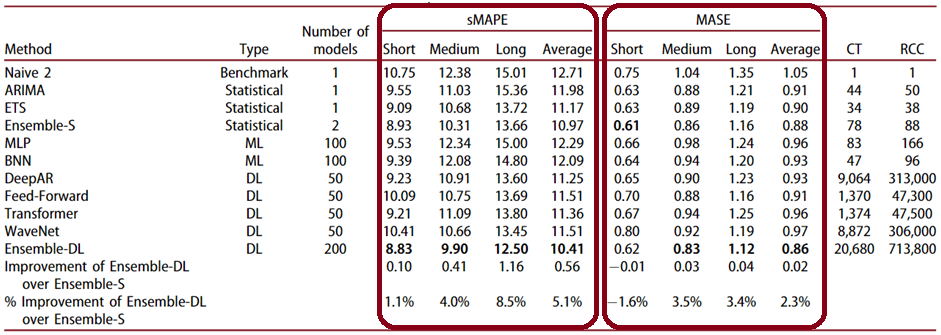
Обычно методы статистического прогнозирования оптимизируются с точки зрения параметров, чтобы свести к минимуму ошибку прогноза на один шаг вперед, например, ETS и ARIMA параметризуются с целью минимизировать внутривыборочную среднеквадратичную ошибку их прогнозов. А MLP и BNN параметризуются с целью получения точных прогнозов на несколько шагов вперед рекурсивным способом.
Таким образом, методы глубокого обучения требуют больше данных для лучшего прогнозирования, особенно когда данные являются нестационарными, имеют сезонность и тенденцию к изменению. Алгоритмы Deep Learning могут эффективно сбалансировать обучение на нескольких горизонтах прогнозирования, жертвуя частью краткосрочной точности, чтобы обеспечить адекватную производительность в долгосрочной перспективе. В свою очередь, статистические модели, обычно хорошо подходят для краткосрочных прогнозов, тогда как алгоритмы Deep Learning лучше отражают долгосрочные характеристики данных. Поэтому целесообразно комбинировать статистические модели и модели машинного обучения с методами Deep Learning в зависимости от временного горизонта прогнозирования, учитывая, что ансамбли работают лучше отдельный нейросетей.
Впрочем, ансамбли даже простых статистических методов, таких как ARIMA, ETS и Theta, часто обеспечивают аналогичную и даже более высокую столь точность прогнозирования на краткосрочном горизонте, чем отдельные DL-модели и их ансамбли. Однако, при среднесрочных или долгосрочных прогнозах статистические методы проигрывают. Обратной стороной высокой точности DL-ансамблей являются дополнительные затраты на их обучение и эксплуатацию. Ансамбли Deep Learning обычно более эффективны при обработке зашумленных данных и трендовых рядов, в отличие от статистических ансамблей, которые обеспечивают более точные прогнозы для сезонных данных, а также для стабильных или линейных рядов. Хотя DL-модели более устойчивы к случайности, сезонность более эффективно учитывается в статистических методах.
Поэтому выбор подходящего алгоритма для анализа данных временных рядов зависит от их особенностей и целей моделирования. Большинство статических алгоритмов машинного обучения, таких как линейная регрессия, SVM, не могут экстраполировать шаблоны и инкапсулировать компоненты временных рядов за пределами области обучающих данных, поскольку они обобщают обучающее пространство для любого нового прогноза. Таким образом, не существует универсального решения для всех случаев прогнозирования временных рядов. Прежде всего, необходимо понять постановку задачи, тип функций, временной горизонт прогнозирования и особенности исследуемых данных.
Как внедрить MLOps-идеи и инструменты в реальные проекты аналитики больших данных и машинного обучения, вы узнаете на специализированных курсах в нашем лицензированном учебном центре обучения и повышения квалификации для разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве:
- Разработка и внедрение ML-решений
- Практическое применение Big Data Аналитики для решения бизнес-задач
Источники

 1236
1236