Содержание
Что такое алгоритм k-medoids, чем он отличается от k-means и как этот метод кластеризации применяется для анализа графов: принципы и инструменты.
Что такое медоид и как устроен алгоритм кластеризации k-medoids
Кластеризация — это метод машинного обучения для поиска кластеров или сообществ в наборе данных. Цель в том, чтобы найти кластеры, в которых наблюдения очень похожи друг на друга, но отличаются от наблюдений в других кластерах. Кластеризация считается алгоритмом машинного обучения без учителя, поскольку идет поиск структуры в наборе данных, а не прогнозирование значения переменной. На практике кластеризация часто используется в маркетинге и в социальных исследованиях, чтобы по демографическим признакам (пол, возраст, доход, образование, профессия и пр.) отнести человека к той или иной категории.
Одним из популярных методов кластеризации считается метод k-средних (k—means). При его простоте и популярности, метод k-means подвержен влияниям выбросов, а его разновидность под названием k-medoids — нет. Алгоритм k—medoids или разделение вокруг медоида был предложен в 1987 году Кауфманом и Руссиу. Медоид – это точка в кластере, различия которой со всеми остальными точками в кластере минимальны. Медоиды близки по смыслу центроидам, но в отличие от них, являются объектом, принадлежащим кластеру, и как правило используются в тех случаях, когда невозможно вычислить средние координаты или центр масс кластера. Алгоритм кластеризации k-medoids, в отличие от k-means на каждой итерации ищет центры кластеров не как среднее точек, а как медоиды точек. То есть, центр кластера должен обязательно являться одной из его точек.
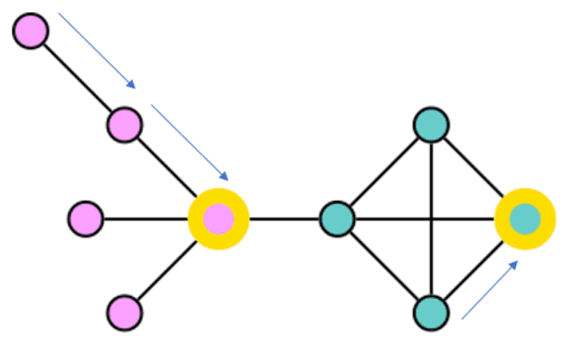
Алгоритм k—medoids пытается оптимизировать выбор медоидов так, чтобы общее расстояние от всех точек данных до ближайшего к ним медоида было как можно меньшим. Метод назначает узлы кластеру на основе кратчайшего пути к медоиду, оптимизируя выбор медоидов так, чтобы создать кратчайшее общее расстояние от узлов графа до ближайшего к ним медоида.
Поскольку k-medoids вычисляет центроиды кластера, используя медианы вместо средних значений, он более устойчив к выбросам по сравнению с k-means. Поэтому, если в наборе данных нет экстремальных выбросов, то k-means и k-medoids будут давать аналогичные результаты.
Таким образом, будучи вариантом популярного метода k-means, алгоритм k-medoids в качестве центроидов использует не любую точку, а только какие-то из имеющихся наблюдений. А, поскольку в графе между вершинами расстояние определено, метод k-medoids отлично подходит для кластеризации графа.
Для реализации k-medoids, как и k-means, требуют определения k — количества выходных кластеров перед запуском алгоритма. Оба алгоритма присваивают каждому члену набора данных один из k-кластеров в зависимости от того, какой кластер имеет ближайший центр к назначенному члену. Ключевое различие между алгоритмами заключается в способе определения этих центров. В k-means центроид, определяющий каждый кластер, представляет собой точку в векторном пространстве со средним значением векторов признаков для элементов в этом кластере. А в k-medoids медоид, определяющий кластер, сам является членом набора данных.
Получается, при кластеризации k-medoids каждое наблюдение в наборе данных помещается в один из k кластеров. Конечная цель в том, чтобы иметь K кластеров, в которых наблюдения внутри каждого кластера очень похожи друг на друга, а наблюдения в разных кластерах сильно отличаются друг от друга. На практике это реализуется следующей последовательностью действий:
- выбор значения k – сколько кластеров надо идентифицировать в данных;
- случайное назначение каждому наблюдению начальному кластеру от 1 до k;
- повтор процедуры, пока назначения кластера не перестанут изменяться. Для каждого из кластеров k надо вычислить центр тяжести кластера – вектор медиан признаков p для наблюдений в k-м кластере. Надо назначить каждое наблюдение кластеру, центроид которого находится ближе всего по евклидову расстоянию.
Таким образом, медоид становится архетипом кластера, помогая понять различия между кластерами на основе этих центральных ориентиров. Поскольку k-medoids требует только знания расстояния между парами элементов в наборе данных, этот метод можно применять непосредственно к данным графа, вычисляя кратчайшие пути между парами узлов. Как это сделать, рассмотрим далее.
Применение медоидов к анализу графов
Чтобы использовать алгоритм k-means для данных графа, нужно представить его топологию в векторном пространстве. Это можно сделать, применив алгоритм внедрения узлов, например, Fast Random Projection, чтобы выразить положение каждого узла в графе в виде вектора. Затем можно рассчитать расстояние между каждым вектором и центроидами кластера, используя евклидово расстояние. Этап внедрения усложняет модель и ухудшает ее интерпретируемость (объяснимость).
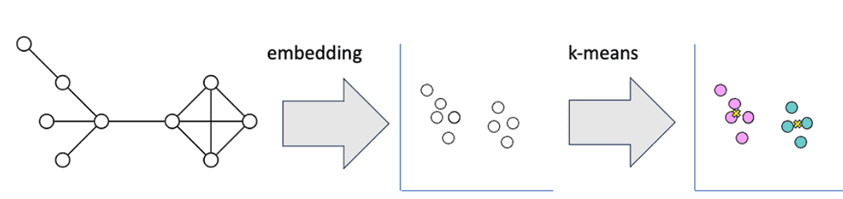
С практической точки зрения поработать с методом k-medoids можно, используя соответствующую библиотеку, например, python-kmedoids. Этот пакет представляет собой обертку быстрого Rust-пакета k-medoids, реализующую алгоритмы FasterPAM и FastPAM, а также базовые алгоритмы k-means-style и PAM. Все алгоритмы ожидают на входе матрицу расстояний, содержащую расстояние между каждой парой элементов в наборе данных, и количество кластеров. Следовательно, их можно использовать с произвольными функциями несходства.
Ключевой сложностью использования k-medoids для данных графа являются затраты на вычисление кратчайшего расстояния между всеми парами узлов графа. Из-за этого ограничения можно эффективно применять этот метод только к небольшим графам из нескольких тысяч узлов или меньше. Для больших графов гораздо более эффективным выбором является быстрое случайное проецирование с использованием k-means. Частично обойти это ограничение можно, применив специализированные алгоритмы вычисления кратчайшего пути, которые есть в инструментах работы с графами. Например, популярная графовая СУБД Neo4j не включает алгоритм k-medoids по умолчанию. Однако, она имеет ряд алгоритмов вычисления путей, представленных в библиотеке Graph Data Science, о которой мы писали здесь.
Поэтому можно использовать Python-пакет kmedoids, отправив ему на вход матрицу расстояний, полученную с помощью алгоритмов расчета кратчайшего пути, поддерживаемых в Graph Data Science. Поскольку любой узел является кандидатом на роль медоида, граф должен быть связным графом. Для этого можно применить методы связанных компонент, о которых мы писали здесь и здесь. Как только будут выявлены связанные компоненты, можно дополнительно сегментировать самые крупные компоненты из них с помощью алгоритмов обнаружения сообществ. Библиотека Graph Data Science в Neo4j включает несколько быстрых алгоритмов обнаружения сообщества: Leiden, Louvain и Label Propagation. Эти алгоритмы идентифицируют сообщества плотно связанных узлов в графе. Но они могут образовывать длинный хвост небольших сообществ в менее связанных частях графа, что следует учитывать при их использовании.
Возвращаясь к алгоритму k-medoids, перечислим его достоинства: простота реализации, быстрая сходимость за фиксированное количество шагов и нечувствительность к выбросам. Однако, алгоритм имеет следующие недостатки:
- подходит для кластеризации только сферических групп объектов, но не произвольных форм. Это связано с тем, что он полагается на минимизацию расстояний между немедоидными объектами и медоидом (центром кластера), используя компактность в качестве критерия кластеризации вместо связности.
- может получить разные результаты для разных прогонов одного и того же набора данных из-за случайного выбора первых k медоидов.
Таким образом, главная проблема метода k-medoids — необходимость явного задания числа кластеров, т.е. оптимальное разбиение на заданное количество частей (graph partitioning). С этим можно бороться двумя путями:
- задавать некую метрику качества разбиения и автоматизировать процесс выбора оптимального числа кластеров;
- раскрашивать граф и визуально определять наиболее логичное разбиение, что подходит только для небольших данных и не более чем для пары десятков кластеров или придется использовать алгоритм с многоуровневой кластеризацией.
Узнайте больше про использование графовых алгоритмов и средств работы с ними для практического применения в реальных проектах аналитики больших данных на специализированных курсах нашего лицензированного учебного центра обучения и повышения квалификации для разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве:
[elementor-template id=»13619″]
Источники

 742
742